排列组合
例 1. 由 0,1,2,3,4,5 可以组成多少个没有重复数字五位奇数?
解析
先排末位共有 $C_3^1$, 然后排首位共有 $C_4^1$, 最后排其它位置共有 $A_4^3$, 由分步计数原理得 $C_4^1 C_3^1 A_4^3=288$ 。
题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列.
例 1. A,B,C,D,E 五人并排站成一排,如果 A,B必须相邻且 B在 A的右边,则不同的排法有( )
A、60 种 B、48 种 C、36 种 D、24 种
解析
把 A,B 视为一人,且 B 固定在 A 的右边,则本题相当于 4 人的全排列,$A_4^4$=24 种, 答案: D .
例 2. 7 人站成一排 ,其中甲乙相邻且丙丁相邻,共有多少种不同的排法.
解析
可先将甲乙两元素捆绑成整体并看成一个复合元素,同时丙丁也看成一个复合元素,再与其它元素进行排列,同时对相邻元素内部进行自排。由分步计数原理可得共有 $A_5^5$$A_2^2$$A_2^2$= 480种不同的排法
元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个 元素插入上述几个元素的空位和两端.
例 1. 七人并排站成一行,如果甲乙两个必须不相邻,那么不同的排法种数是( )
A、1440 种 B、3600 种 C、4820 种 D、4800 种
解析
除甲乙外,其余 5 个排列数为$A_5^5$种,再用甲乙去插 6 个空位有$A_6^2$种,不同的排法种数是$A_5^5$$A_6^2$=3600 种, 选 B.
例 2. 某人射击八枪,命中四枪,四枪中恰好有三枪连在一起的情形的不同种数为?
解析
把连续命中的三枪看做一个整体a,剩下命中的一枪看做一个整体b,用插空法,把a,b两个元素按一定顺序插到剩下四枪形成的5个空隙里,是$A_5^2$=20
例 1. 7 人排队,其中甲乙丙 3 人顺序一定(可以不相邻),共有多少不同的排法?
解析
(倍缩法) 对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不 同排法种数是: $A_7^7 / A_3^3$
(空位法) 设想有7把椅子让除甲乙丙以外的四人就坐共有$A_7^4$ 种方法,其余的三个位置甲乙丙共有(1)种坐法,则共有$A_7^4$ 种方法。
有序分配问题指把元素分成若干组,可用逐步下量分组法.
例 1. 有甲乙丙三项任务,甲需 2 人承担,乙丙各需一人承担,从 10 人中选出 4 人承担这三项任务,不同的选法种数是( )
A、1260 种 B、2025 种 C、2520 种 D、5040 种
解析
先从 10 人中选出 2 人承担甲项任务,再从剩下的 8 人中选 1 人承担乙项任务,第三步从另外的 7 人中选1 人承担丙项任务,不同的选法共有 $C_{10}^{2}$$C_8^1$$C_7^1$=2520 种,选 C.
例 2. 12 名同学分别到三个不同的路口进行流量的调查,若每个路口 4 人,则不同的分配方案有( A)
A、$C_{12}^{4}$$C_8^4$$C_4^4$ 种 B、3$C_{12}^{4}$$C_8^4$$C_4^4$ 种 C、$C_{12}^{4}$$C_8^4$$A_3^3$ 种 D、$\frac{C_{12}^{4}C_8^4C_4^4}{A_3^3}$ 种
例 1. 4 名优秀学生全部保送到 3 所学校去,每所学校至少去一名,则不同的保送方案有多少种?
解析
把四名学生分成 3 组有 $C_4^2$ 种方法,再把三组学生分配到三所学校有 $A_3^3$ 种,故共有 $C_4^2$$A_3^3$=36 种方法.
例 2. 5 本不同的书,全部分给 4 个学生,每个学生至少一本,不同的分法种数为( )
A、480 种 B、240 种 C、120 种 D、96 种
解析
B. $C_5^3$$A_4^4$=240
例 1: 10 个三好学生名额分到 7 个班级,每个班级至少一个名额,有多少种不同分配方案?
解析
10 个名额分到 7 个班级,就是把 10 个名额看成 10 个相同的小球分成 7 堆,每堆至少一个,可以在 10 个小球的 9 个空位中插入 6 块木板,每一种插法对应着一种分配方案,故共有不同的分配方案为$C_9^6$=84 种.
例 2: 若x+y+z+w=100,求这个方程组的自然数解的组数.
解析
我们认为0是自然数,所有存在0+0+0+100=100的情况,所以这里的元素 个数应为104个,即3个 0和100个1,这104个元素间有103个空位,中间插入 4个隔板,就会把这104个元素分成4堆,每堆对应 x,y,x,w,而挡板的放置方法有$C_{103}^{3}$
例 1. 某高校从某系的 10 名优秀毕业生中选 4 人分别到西部四城市参加中国西部经济开发建设,其中甲同学不到银川,乙不到西宁,共有多少种不同派遣方案?
解析
因为甲乙有限制条件,所以按照是否含有甲乙来分类,有以下四种情况: ①若甲乙都不参加,则有派遣方案 $A_8^4$ 种;②若甲参加而乙不参加,先安排甲有 3 种方法,然后安排其余学生有 $A_8^3$方法,所以共有 3$A_8^3$;③若乙参加而甲不参加同理也有 3$A_8^3$种;④若甲乙都参加,则先安排甲乙,有 7 种方法, 然 后 再 安 排 其 余 8 人 到 另 外 两 个 城 市 有 $A_8^2$种 , 共 有 7$A_8^2$方 法 . 所 以 共 有 不 同 的 派 遣 方 法 总 数 为 $A_8^4$ + 3$A_8^3$ + 3$A_8^3$ + 7$A_8^2$=4088 种.
例 1 (1)由数字 0,1,2,3,4,5 组成没有重复数字的六位数,其中个位数字小于十位数字的共有( )
A、210 种 B、300 种 C、464 种 D、600 种
(2)从 1,2,3…,100 这 100 个数中,任取两个数,使它们的乘积能被 7 整除,这两个数的取法(不计顺序)共有多少种?
(3)从 1,2,3,…,100 这 100 个数中任取两个数,使其和能被 4 整除的取法(不计顺序)有多少种?
解析
(1)按题意,个位数字只可能是 0,1,2,3,4 共 5 种情况,分别有 $A_5^5$个,$A_4^1$$A_3^1$$A_3^3$ , $A_3^1$$A_3^1$$A_3^3$ , $A_2^1$$A_3^1$$A_3^3$ , $A_3^1$$A_3^3$个,合并总计 300 个,选 B.
(2)被取的两个数中至少有一个能被 7 整除时,他们的乘积就能被 7 整除,将这 100 个数组成的集合视为全集I,能被 7 整除的数的集合记做 $\overline{A}$ = { 7,14,21,$\cdots$,98 } 共有 14 个元素,不能被 7 整除的数组成的集合记做 $\overline{A}$ = { 1,2,3,4,$\cdots$,100 } 共有 86 个元素;由此可知,从 A中任取 2 个元素的取法有 $C_{14}^{2}$,从 A中任取一个,又从$\overline{A}$中任取一个共有 $C_{14}^{1}$$C_{86}^{1}$,两种情形共符合要求的取法有 $C_{14}^{2}$ + $C_{14}^{1}$$C_{86}^{1}$=1295 种.
(3)将 I = { 1,2,3,$\cdots$,100 } 分成四个不相交的子集,能被 4 整除的数集 A = { 4,8,12,$\cdots$,100 };能被 4 除余 1 的数集B = { 1,5,9,$\cdots$,97 } ,能被 4 除余 2 的数集 C = { 2,6,$\cdots$,98 } ,能被 4 除余 3 的数集 D = { 3,7,11,$\cdots$,99 } ,易见这四个集合中每一个有 25 个元素;从 A中任取两个数符合要;从B,D 中各取一个数也符合要求;从 C中任取两个数也符合要求;此外其它取法都不符合要求;所以符合要求的取法共有 $C_{25}^{2}$ + $C_{25}^{1}$$C_{25}^{1}$ + $C_{25}^{2}$ 种.
例 1. 从 6 名运动员中选出 4 人参加 4×100 米接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同的参赛方案?
解析
设全集= {6 人中任取 4 人参赛的排列} ,A={甲跑第一棒的排列} ,B={乙跑第四棒的排列} ,根据求集合元素个数的公式得参赛方法共有: n(I)-n(A)-n(B)+n(A $\cap$ B ) = $A_6^4$-$A_5^3$-$A_5^3$+$A_4^2$ = 252
例 1. 5双相异的鞋共10只,现随机地取出6只,恰好能配成2双鞋的取法是多少?
解析
$C_{5}^{2} C_{6}^{1} C_{4}^{1}$=240
例 1. 8人排成前后两排,每排4人,其中甲乙在前排,丙在后排,共有多少排法?
解析
看成一排,某 2 个元素在前半段四个位置中选排 2 个,有 $A_4^2$种,某 1 个元素排在后半段的四个位置中选一个有 $A_4^1$种,其余 5 个元素任排 5 个位置上有 $A_5^5$种,故共有 $A_4^2$$A_4^1$$A_5^5$=5760 种排法.
例 1. 从 4 台甲型和 5 台乙型电视机中任取 3 台,其中至少要甲型和乙 型电视机各一台,则不同的取法共有( )
A、140 种 B、80 种 C、70 种 D、35 种
解析
至少要甲型和乙 型电视机各一台可分两种情况:甲型 1 台乙型 2 台;甲型 2 台乙型 1 台;故不同的取法有 $C_5^2$$C_4^1$ + $C_5^1$$C_4^2$ =70 台,选 C.
例 1. (1)以正方体的顶点为顶点的四面体共有( )
A、70 种 B、64 种 C、58 种 D、52 种
(2)四面体的顶点和各棱中点共 10 点,在其中取 4 个不共面的点,不同的取法共有( )
A、150 种 B、147 种 C、144 种 D、141 种
解析
(1)正方体 8 个顶点从中每次取四点,理论上可构成 $C_8^4$四面体,但 6 个表面和 6 个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有$C_8^4$-12= 58 个.
(2)10 个点中任取 4 个点共有 $C_{10}^{4}$种,其中四点共面的有三种情况:①在四面体的四个面上,每面内四点共面的情况为 $C_6^4$,四个面共有 4$C_6^4$个;②过空间四边形各边中点的平行四边形共 3 个;③过棱上三点与对棱中点的三角形共 6 个.所以四点不共面的情况的种数是 $C_{10}^{4}$ - 4$C_6^4$ -3-6=141 种.
例 1. 把 6 名实习生分配到 7 个车间实习共有多少种不同方法?
解析
完成此事共分 6 步,第一步;将第一名实习生分配到车间有 7 种不同方案,第二步:将第二名实习生分配到车间也有 7 种不同方案,依次类推,由分步计数原理知共有 $A_{7}^{6}$种不同方案.
例 1. 10级台阶,某人可一步跨一级,也可跨两级,也可跨三级。 (1)他6步就可上完台阶的方法数是多少? (2)他上完台阶的方法总数是多少?
解析
(1)按照 3,3,1,1,1,1 的走法有 $C_{6}^{2}$ 种,按照 3,2,2,1,1,1 的走法有 $C_{6}^{1} C_{5}^{2}$ 种,按照 2,2,2,2,1,1 的走法有 $C_{6}^{4}$ 种,所以恰好6步上完台阶的方法种数是 $C_{6}^{2}$+$C_{6}^{1} C_{5}^{2}$+$C_{6}^{4}$=15+60+15=90 .
(2)上楼梯问题是典型的斐波那契数列,设爬n级台阶的解法总数为f(n),因为规定每一步只能跨一级或两级或三级,则f(n)=f(n-1)+f(n-2)+f(n-3)。易知f(1)=1,f(2)=2,f(3)=4,递推可得f(4)=7,f(5)=13,f(6)=24,f(7)=44,f(8)=81,f(9)=149,f10)=274
例 1. 设有编号为 1,2,3,4,5 的五个球和编号为 1,2,3,4,5 的盒子现将这 5 个球投入 5 个盒子要求每个盒子放一个球,并且恰好有两个球的号码与盒子号码相同,问有多少种不同的方法?
解析
从 5 个球中取出 2 个与盒子对号有 $C_5^2$种,还剩下 3 个球与 3 个盒子序号不能对应,利用枚举法分析,如果剩下 3,4,5 号球与 3,4,5 号盒子时,3 号球不能装入 3 号盒子,当 3 号球装入 4 号盒子时,4,5 号球只有1 种装法,3 号球装入 5 号盒子时,4,5 号球也只有 1 种装法,所以剩下三球只有 2 种装法,因此总共装法数为2$C_5^2$= 20 种.
例 1.(1)30030 能被多少个不同偶数整除?
(2)正方体 8 个顶点可连成多少队异面直线?
解析
(1)先把 30030 分解成质因数的形式:30030=2×3×5×7×11×13;依题意偶因数 2 必取,3,5,7,11,13这 5 个因数中任取若干个组成成积,所有的偶因数为$C_5^0$+$C_5^1$+$C_5^2$+$C_5^3$+$C_5^4$+$C_5^5$= 32 个.
(2)因为四面体中仅有 3 对异面直线,可将问题分解成正方体的 8 个顶点可构成多少个不同的四面体,从正方体 8 个顶点中任取四个顶点构成的四面体有$C_8^4$-12= 58 个,所以 8 个顶点可连成的异面直线有 3×58=174 对.
例 1. (1)圆周上有 10 点,以这些点为端点的弦相交于圆内的交点有多少个?
(2)某城市的街区有 12 个全等的矩形组成,其中实线表示马路,从 A到 B的最短路径有多少种?
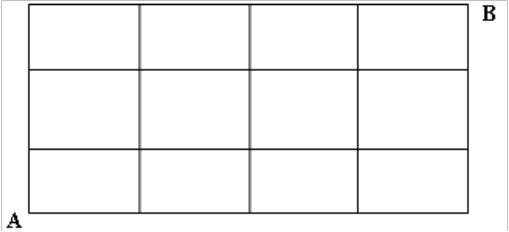
解析
(1)因为圆的一个内接四边形的两条对角线相交于圆内一点,一个圆的内接四边形就对应着两条弦相交于圆内的一个交点,于是问题就转化为圆周上的 10 个点可以确定多少个不同的四边形,显然有 $C_{10}^{4}$个,所以圆周上有10 点,以这些点为端点的弦相交于圆内的交点有 $C_{10}^{4}$个.
(2)可将图中矩形的一边叫一小段,从 A到 B最短路线必须走 7 小段,其中:向东 4 段,向北 3 段;而且前一段的尾接后一段的首,所以只要确定向东走过 4 段的走法,便能确定路径,因此不同走法有 $C_{7}^{4}$种.
例 1. 分别编有 1,2,3,4,5 号码的人与椅,其中i 号人不坐i 号椅(i = 1,2,3,4,5)的不同坐法有多少种?
解析
全错位排列是组合数学中的经典问题之一,使用公式不容易出错: $$ D(n)=(n-1) \cdot[D(n-1)+D(n-2)] . $$ 又易知, $D(1)=0, D(2)=1$. 由递推公式可得: $D(3)=2, D(4)=9,D(5)=44$
例 1. 8 人围桌而坐,共有多少种坐法?
解析
$\mathrm{n}$ 个不同元素作圆形排列,共有 $(\mathrm{n}-1)$!种排法.即7! 如果从 $\mathrm{n}$ 个不同元素中取出 $\mathrm{m}$ 个元素作圆形排列共有 $\frac{1}{n} A_n^m$ 。
例 1. 从 0,1,2,3,4,5,6,7,8,9 这十个数字中取出三个数,使其和为不小于 10 的 偶数,不同的取法有多少种?
解析
这问题中如果直接求不小于 10 的偶数很困难, 可用总体淘汰法。这十个数字 中有 5 个偶数 5 个奇数, 所取的三个数含有 3 个偶数的取法有 $C_5^3$, 只含有 1 个偶数 的取法有 $C_5^1 C_5^2$, 和为偶数的取法共有 $C_5^1 C_5^2+C_5^3$ 。再淘汰和小于 10 的偶数共 9 种, 符合条件的取法共有 $C_5^1 C_5^2+C_5^3-9$
例 1. 6 本不同的书平均分成 3 堆,每堆 2 本共有多少分法?
解析
分三步取书得 $C_6^2 C_4^2 C_2^2$ 种方法, 但这里出现重复计数的现象, 不妨记 6 本书为 $A B C D E F$, 若第一步取 $A B$, 第二步取 $C D$, 第三步取 $E F$ 该分法记为 (AB, $C D, E F)$, 则 $C_6^2 C_4^2 C_2^2$ 中还有 (AB, $\left.\mathrm{EF}, \mathrm{CD}\right)$, (CD, AB, $\mathrm{EF}$ ), (CD, EF, AB) (EF, CD, AB), (EF, AB, CD) 共有 $A_3^3$ 种取法, 而这些分法仅是 ( $\left.\mathrm{AB}, \mathrm{CD}, \mathrm{EF}\right)$ 一种分法, 故共有 $C_6^2 C_4^2 C_2^2 / A_3^3$ 种分法。
例 1. 有红、黄、兰色的球各 5 只,分别标有 A、B、C、D、E 五个字母,现从中取 5 只,要求各字母均有且三色齐备,则共有多少种不同的取法
解析
按颜色分有1 1 3和1 2 2 两种,各3种方案。2.分字母,1 1 3对应有$C_5^1$$C_4^1$$C_3^3$共20种,1 2 2对应$C_5^1$$C_4^2$$C_2^2$共30种,320+330=150
例 2. 在一次演唱会上共 10 名演员,其中 8 人能能唱歌,5 人会跳舞,现要演出一个 2 人唱歌 2 人伴舞的节目,有多少选派方法?
解析
10 演员中有 5 人只会唱歌, 2 人只会跳舞 3 人为全能演员。选上唱歌人员为 标准进行研究只会唱的 5 人中没有人选上唱歌人员共有 $C_3^2 C_3^2$ 种, 只会唱的 5 人中只 有 1 人选上唱歌人员 $C_5^1 C_3^1 C_4^2$ 种, 只会唱的 5 人中只有 2 人选上唱歌人员有 $C_5^2 C_5^2$ 种, 由分类计数原理共有 $C_3^2 C_3^2+C_5^1 C_3^1 C_4^2+C_5^2 C_5^2$ 种。